相手のバトルポケモンをどくとねむりにする
2018年3月2日 ポケモンカードゲーム
ビビヨンの「ビビッドパウダー」は割がいいのか重回帰分析してみる。
「ビビッドパウダー」は「相手のバトルポケモンをどくとねむりにする」という効果で、さらに50ダメージを与える。
1エネで50ダメは割が良い気がするが、
しかし2進化ポケモンでもある。
実際のところ効率はどうなのかを考えてみたい。
まず、ワザを使うための条件として以下の3つがある
・そのポケモンを場に出す
・エネルギーをつける
・コイントスをする
つまりダメージは
・必要なポケモンの数
・必要なエネルギーの数
・コイントスの数
の3つのコストに依存する利得であり、それは三元の関数で表現できる。
今回はこれまでの同様の効果をもつカードを重回帰分析し、回帰式を求めてみる。
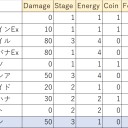
スタンダードレギュレーションで相手をどくとねむりにできるカードは
・フシギバナEX
・ジュカインEX
・ゴース
・ドクケイル
重回帰分析をするにはちょっと心もとないので、
エクストラレギュの
・ケムッソ
・ラフレシア
殿堂レギュの
・ロズレイド
・クサイハナ
・ゴースト
を加えた9枚を使って行う。
計算は割愛するが回帰式は
D = -4.375S + 22.589E - 0.625C - 12.143
が得られる。
この時
D:ダメージ
S:進化するために必要なポケモンカード(たね:1、2進化:3)
E:エネルギーの数
C:コイントスの回数
である
禁断の光のビビヨンは
・2進化ポケモンなので3枚
・エネルギーは1枚
・コイントスは0回
であるから
D = -4.375*3 + 22.589*1 - 0.625*0 - 12.143 ≒ -2.679
となり、今回のビビヨンはこれまでの傾向から言えば「ダメージなし」が相当で
この回帰式では、2進化であることを勘案しても、
1エネ&コイントスなしで効果付き50ダメージは破格と言える。
でも、「どく」と「ねむり」にしたからと言ってどうなるのかは別の話か。
「ビビッドパウダー」は「相手のバトルポケモンをどくとねむりにする」という効果で、さらに50ダメージを与える。
1エネで50ダメは割が良い気がするが、
しかし2進化ポケモンでもある。
実際のところ効率はどうなのかを考えてみたい。
まず、ワザを使うための条件として以下の3つがある
・そのポケモンを場に出す
・エネルギーをつける
・コイントスをする
つまりダメージは
・必要なポケモンの数
・必要なエネルギーの数
・コイントスの数
の3つのコストに依存する利得であり、それは三元の関数で表現できる。
今回はこれまでの同様の効果をもつカードを重回帰分析し、回帰式を求めてみる。
スタンダードレギュレーションで相手をどくとねむりにできるカードは
・フシギバナEX
・ジュカインEX
・ゴース
・ドクケイル
重回帰分析をするにはちょっと心もとないので、
エクストラレギュの
・ケムッソ
・ラフレシア
殿堂レギュの
・ロズレイド
・クサイハナ
・ゴースト
を加えた9枚を使って行う。
計算は割愛するが回帰式は
D = -4.375S + 22.589E - 0.625C - 12.143
が得られる。
この時
D:ダメージ
S:進化するために必要なポケモンカード(たね:1、2進化:3)
E:エネルギーの数
C:コイントスの回数
である
禁断の光のビビヨンは
・2進化ポケモンなので3枚
・エネルギーは1枚
・コイントスは0回
であるから
D = -4.375*3 + 22.589*1 - 0.625*0 - 12.143 ≒ -2.679
となり、今回のビビヨンはこれまでの傾向から言えば「ダメージなし」が相当で
この回帰式では、2進化であることを勘案しても、
1エネ&コイントスなしで効果付き50ダメージは破格と言える。
でも、「どく」と「ねむり」にしたからと言ってどうなるのかは別の話か。
マッドマウンテンとしょうりのほし
2017年6月7日 ポケモンカードゲーム
コインを2枚投げてその両方がオモテになる確率は
1/2 x 1/2 = 1/4
で25%である。
もし、この時、ウラが出た時に一度だけコインを投げなおして良いとなった場合の確率は幾らだろうか。
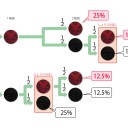
今回は試行回数が少ないので樹形図で見てみる。
1度の降り直しが可能な状態で、2度のコイントスの結果は図の通り6パターンになる。
A. 1枚目が表、2枚目も表
B. 1枚目が表、2枚目が裏で、振りなおして表
C. 1枚目が表、2枚目が裏で、振りなおして裏
D. 1枚目が裏で、振りなおして表、2枚目が表
E. 1枚目が裏で、振りなおして表、2枚目が裏
F. 1枚目が裏で、振りなおしても裏
このうち、2回とも表になるパターンは以下の3つ
A. 1枚目が表、2枚目も表
B. 1枚目が表、2枚目が裏で、振りなおして表
D. 1枚目が裏で、振りなおして表、2枚目が表
判定はコイントスのみで、その確率は他に影響されず、常に1/2であるから、
投げたコインの回数nとして、それぞれの状態になる確率は「1/2のn乗」である。
すなわち、それぞれ
A. (1/2)^2 = 1/4 = 25%
B. (1/2)^3 = 1/8 = 12.5%
D. (1/2)^3 = 1/8 = 12.5%
よって、表題の成功率は、25%+12.5%+12.5%=50%
ビクティニがいれば、サイドンのマッドマウンテンを、コイントス1回分で成功させられるわけだ。
1/2 x 1/2 = 1/4
で25%である。
もし、この時、ウラが出た時に一度だけコインを投げなおして良いとなった場合の確率は幾らだろうか。
今回は試行回数が少ないので樹形図で見てみる。
1度の降り直しが可能な状態で、2度のコイントスの結果は図の通り6パターンになる。
A. 1枚目が表、2枚目も表
B. 1枚目が表、2枚目が裏で、振りなおして表
C. 1枚目が表、2枚目が裏で、振りなおして裏
D. 1枚目が裏で、振りなおして表、2枚目が表
E. 1枚目が裏で、振りなおして表、2枚目が裏
F. 1枚目が裏で、振りなおしても裏
このうち、2回とも表になるパターンは以下の3つ
A. 1枚目が表、2枚目も表
B. 1枚目が表、2枚目が裏で、振りなおして表
D. 1枚目が裏で、振りなおして表、2枚目が表
判定はコイントスのみで、その確率は他に影響されず、常に1/2であるから、
投げたコインの回数nとして、それぞれの状態になる確率は「1/2のn乗」である。
すなわち、それぞれ
A. (1/2)^2 = 1/4 = 25%
B. (1/2)^3 = 1/8 = 12.5%
D. (1/2)^3 = 1/8 = 12.5%
よって、表題の成功率は、25%+12.5%+12.5%=50%
ビクティニがいれば、サイドンのマッドマウンテンを、コイントス1回分で成功させられるわけだ。
ポケモンバトルにおける確定数の新たな概算方法の提案(導出)
2017年5月26日 ゲーム先のブログで確定数を足し算引き算だけで概算する方法を示したが、それの数学的思考を示す。
Lv50戦で、攻撃ステの実値がaのポケモンAが防御ステ実値dのポケモンDにタイプ一致威力110の技で与えるダメージDmgは以下の式で求められる。
Dmg = ((22×110×a) / (50×d) + 2)×1.5 = (363a)/(5d)+3
※実際にはこれにダメージ乱数(0.85~1.00)をかけるが今は1.00とする
ポケモンAがポケモンDを倒すのに必要な攻撃回数nはポケモンDのHPをこのダメージDmgで割ってやればよい。
例によって+3の項は十分無視できるとし、HPをhすると、
n = h/Dmg = h/{(363a)/(5d)} = (5hd)/(363a) … ①
とあるポケモンVのHP、攻撃ステ、防御ステがそれぞれ、p,q,rとする。
この時、ポケモンVはポケモンVを1回の攻撃で倒せるとすると、①式に代入して
n = (5pr)/(363q) = 1 … ②
が成り立つ。②から、①式は以下のように変形できる
n = (5hd)/(363a) = {(5pr)/(363a)}×{(5hd)/(363q)}
この時、①より{(5pr)/(363a)}はポケモンAがポケモンVを倒すまでの攻撃回数を、
{(5hd)/(363q)}はポケモンVがポケモンDを倒すまでの攻撃回数を表す。
つまりこれは、以下の情報が分かっていれば「ポケモンAはポケモンDを何回の攻撃で倒せるか」がわかることを示している。
・ポケモンAはポケモンVをx回の攻撃で倒せる
・ポケモンVはポケモンVを1回の攻撃で倒せる
・ポケモンVはポケモンDをy回の攻撃で倒せる
代表となるポケモンVは②が満たせればなんでもよい。
例えば、ここでは私の嫁のビビヨン(p=156, q=155, r=72)で考える。
ポケモンAがポケモンV(ビビヨン)を倒すのに必要な攻撃回数nAは
nA = {(5pr)/(363a)} = 18720/(121a) … ③
ポケモンV(ビビヨン)がポケモンDを倒すのに必要な攻撃回数nDは
nD = {(5hd)/(363q)} = (hd)/11253 … ④
になる。
要するにある代表ポケモンを1匹定め、それぞれが代表ポケモンに対する攻撃回数nA,nDで火力、耐久指数を種族値の代わりに覚えておけば対戦中に1回の四則演算で必要な攻撃回数を求められるという事だ。
ただ、この時、実数の掛け算が生じる。計算の早い人ならすぐ出来るかも知れないが私はやりたくない。
そこでこれを足し算引き算で表せるように対数を取る。この時の底は、「2の7乗根」とした。
この「2の7乗根」は2乗するとおよそ1.2、3乗するとおよそ1.3、4乗するとおよそ1.5というポケモンで多く使われる数字に近似する特性がある。
上記の式③、④の対数を取り整理するとそれぞれ以下の式⑤、⑥が得られる
log(nA,2^(1/7)) = log(18720/(121a),2^(1/7))=7*log(18720/(121a))/log(2) … ⑤
log(nD,2^(1/7)) = log((hd)/11253,2^(1/7))=7*log((hd)/11253)/log(2) … ⑥
これが評価値となる。
例えばカプ・テテフの場合Cについて無振りの場合150、極振りの場合182になる。
これを上記の式⑤、⑥に代入するとそれぞれ-0.31、1.64という数字が得られる。
これを防御側の値と攻撃側の値を加算して0になれば攻撃回数が1回ということになる。
使用に際して0.5刻み程度で丸めた方がいいかもしれない(-0.31→-0.5、1.64→1.5)
また、この時火力については実値が高いほど小さな数字が出て感覚的ではないので-1をかけた方がよいかもしれない。
Lv50戦で、攻撃ステの実値がaのポケモンAが防御ステ実値dのポケモンDにタイプ一致威力110の技で与えるダメージDmgは以下の式で求められる。
Dmg = ((22×110×a) / (50×d) + 2)×1.5 = (363a)/(5d)+3
※実際にはこれにダメージ乱数(0.85~1.00)をかけるが今は1.00とする
ポケモンAがポケモンDを倒すのに必要な攻撃回数nはポケモンDのHPをこのダメージDmgで割ってやればよい。
例によって+3の項は十分無視できるとし、HPをhすると、
n = h/Dmg = h/{(363a)/(5d)} = (5hd)/(363a) … ①
とあるポケモンVのHP、攻撃ステ、防御ステがそれぞれ、p,q,rとする。
この時、ポケモンVはポケモンVを1回の攻撃で倒せるとすると、①式に代入して
n = (5pr)/(363q) = 1 … ②
が成り立つ。②から、①式は以下のように変形できる
n = (5hd)/(363a) = {(5pr)/(363a)}×{(5hd)/(363q)}
この時、①より{(5pr)/(363a)}はポケモンAがポケモンVを倒すまでの攻撃回数を、
{(5hd)/(363q)}はポケモンVがポケモンDを倒すまでの攻撃回数を表す。
つまりこれは、以下の情報が分かっていれば「ポケモンAはポケモンDを何回の攻撃で倒せるか」がわかることを示している。
・ポケモンAはポケモンVをx回の攻撃で倒せる
・ポケモンVはポケモンVを1回の攻撃で倒せる
・ポケモンVはポケモンDをy回の攻撃で倒せる
代表となるポケモンVは②が満たせればなんでもよい。
例えば、ここでは私の嫁のビビヨン(p=156, q=155, r=72)で考える。
ポケモンAがポケモンV(ビビヨン)を倒すのに必要な攻撃回数nAは
nA = {(5pr)/(363a)} = 18720/(121a) … ③
ポケモンV(ビビヨン)がポケモンDを倒すのに必要な攻撃回数nDは
nD = {(5hd)/(363q)} = (hd)/11253 … ④
になる。
要するにある代表ポケモンを1匹定め、それぞれが代表ポケモンに対する攻撃回数nA,nDで火力、耐久指数を種族値の代わりに覚えておけば対戦中に1回の四則演算で必要な攻撃回数を求められるという事だ。
ただ、この時、実数の掛け算が生じる。計算の早い人ならすぐ出来るかも知れないが私はやりたくない。
そこでこれを足し算引き算で表せるように対数を取る。この時の底は、「2の7乗根」とした。
この「2の7乗根」は2乗するとおよそ1.2、3乗するとおよそ1.3、4乗するとおよそ1.5というポケモンで多く使われる数字に近似する特性がある。
上記の式③、④の対数を取り整理するとそれぞれ以下の式⑤、⑥が得られる
log(nA,2^(1/7)) = log(18720/(121a),2^(1/7))=7*log(18720/(121a))/log(2) … ⑤
log(nD,2^(1/7)) = log((hd)/11253,2^(1/7))=7*log((hd)/11253)/log(2) … ⑥
これが評価値となる。
例えばカプ・テテフの場合Cについて無振りの場合150、極振りの場合182になる。
これを上記の式⑤、⑥に代入するとそれぞれ-0.31、1.64という数字が得られる。
これを防御側の値と攻撃側の値を加算して0になれば攻撃回数が1回ということになる。
使用に際して0.5刻み程度で丸めた方がいいかもしれない(-0.31→-0.5、1.64→1.5)
また、この時火力については実値が高いほど小さな数字が出て感覚的ではないので-1をかけた方がよいかもしれない。
ポケモンバトルにおける確定数の新たな概算方法の提案
2017年5月25日 ゲーム
時間制限があるバトルで、対戦中に相手を倒せるか(または倒されるか)を足し算引き算だけで概算する方法を考えている。
※負値はわかりにくいとの指摘があったのでそのうち調整します
~背景~
従来の種族値ベースの考え方に私は限界を感じている。
対戦中知りたいのは「あと何回の攻撃で相手は倒れるか」「次の攻撃で自分は倒れるか」ではなかろうか。
しかし、これを計算するためには「種族値」→「実値」→「ダメージ」→「割合」「回数」という順で計算しなくてはいけない。あっという間に60秒が過ぎる。
もっと別の指標で対戦時の優劣を表現できないものか。
次の攻撃で倒せるかどうか概算する方法がないか。
できるだけ簡単に。
~概要~
種族値などに代えて、それぞれのポケモン実値から画像の表のように評価値で表す。
(この表の求め方および数学的思考過程については次の記事で詳しく説明する)
例としてWCSルールシーズン3のポケモンTOP5は以下のようになる(0振り~252振り/性格補正なし)。
ウインディ
物理火力:☆-2.0~ ☆0.5
物理耐久:☆4.0~ ☆8.5
特殊火力:☆-2.5~ ☆0.0
特殊耐久:☆4.0~ ☆8.5
ガブリアス
物理火力:☆-0.5~ ☆1.5
物理耐久: ☆6.5~ ☆10.5
特殊火力:☆-4.5~ ☆-1.5
特殊耐久: ☆5.5~ ☆9.5
カプ・コケコ
物理火力:☆-1.5~ ☆1.0
物理耐久:☆3.0~ ☆8.0
特殊火力:☆-3.0~ ☆-0.5
特殊耐久:☆2.0~ ☆7.0
カプ・テテフ
物理火力:☆-4.0~ ☆-1.0
物理耐久:☆2.0~ ☆7.0
特殊火力:☆-0.5~ ☆1.5
特殊耐久:☆5.5~ ☆10.0
カミツルギ
物理火力:☆2.5~ ☆4.0
物理耐久:☆6.0~ ☆10.0
特殊火力:☆-7.0~ ☆-3.5
特殊耐久:☆-5.0~ ☆2.0
残念ながら、どのポケモンがどの程度の評価値なのかは種族値のように覚えなければならない。
この評価値で実際に計算してみる。計算は以下のルールで行う。
ルール①
相手の耐久評価値から、攻撃側の火力評価値を引く。
その時に0以下になれば倒せる事を意味する。
実例でやってみよう。
「カプ・コケコのかみなりで、ウインディを倒せるか」
カプ・コケコの極振りで☆-0.5、対してウインディの特殊耐久は無振りで4.0。
☆4.0から☆-0.5を引いて☆4.5、☆0より大きいので倒せない。
ちなみに割合を知りたい時は、計算結果によって大雑把に以下のようになる
☆0: HPの100%程度
☆1: HPの90%程度
☆2: HPの80%程度
☆3: HPの75%程度
☆4: HPの70%弱程度
☆5: HPの60%程度
また、確定数は引いた結果から以下のようになる。
~☆0 確1
~☆7 確2
~☆11 確3
~☆14 確4
今回は☆4.5なので相手HPを65%程度削って確2と言ったところか。
実際にダメ計すると
攻: カプ・コケコ Lv.50
防: ウインディ Lv.50
ダメージ: 93~109
割合: 56.3%~66%
回数: 確定2発
威力: 110
タイプ: でんき*/特殊
特攻: 147
特防: 100
最大HP: 165
で確かに最高乱数で66%になる。
ダメ―ジ乱数やその他もろもろの倍率は以下のように処理する。全部足し算引き算でできる。
ルール② 倍率計算時
2.0倍(弱点、2段階上昇等):☆7を足す
1.5倍(拘り、輝石、1段階上昇等):☆4を足す
1.3倍(珠等):☆3を足す
1.2倍(プレート等):☆2を足す
1.1倍(性格上昇補正等):☆1を足す
0.9倍(性格下降補正等):☆1を引く
2/3倍(威嚇、タイプ不一致、1段階下降等):☆4を引く
1/2倍(やけど、2段階下降等):☆7を引く
ルール③ 技の威力
120 攻撃側から☆1を足す
110 そのまま
100 攻撃側から☆1を引く
90 攻撃側から☆2を引く
80 攻撃側から☆3を引く
75 攻撃側から☆4を引く
ルール④ ダメージ乱数
低乱数(5%程度):そのまま
中乱数(30%程度):攻撃側から☆0.5を引く
中乱数(60%程度):攻撃側から☆1.0を引く
高乱数(90%程度):攻撃側から☆1.5を引く
実例でやってみよう。
「カプ・テテフがサイコフィールドを張っている。サイコキネシスでカミツルギを倒せるだろうか」
カプ・テテフの極振りで特殊火力は☆1.5、
サイキネは威力90なので☆2つ減らす→☆0.5
サイコフィールドの効果で1.5倍なので☆4つ増やす→☆4.5
半減なので☆7つ減らす→☆-3.5
高乱数で考えたいので☆1.5減らす→☆-5.0
カミツルギの特殊耐久は☆-5.0~☆2.0
カミツルギの特殊耐久が無振りであれば☆-5.0から☆-5.0を引いて☆0。
☆0はピッタリ確1くらいの打点ということ。
ダメ計すると
攻: カプ・テテフ Lv.50
防: カミツルギ Lv.50
ダメージ: 135~159
割合: 100.7%~118.6%
回数: 確定1発
技: サイコキネシス
威力: 135 [サイコ]
タイプ: エスパー*/特殊
特攻: 182
特防: 51
最大HP: 134
相性: ×0.5
丁度確1である。
恐らくこれまでとは全く異なる計算体系で慣れるまで抵抗もあるだろうし、
あくまで概算なのでギリギリの時には誤差を生じる恐れもある。
しかし、実戦では指折り数えることで計算できるので、
種族値ベースでダメ計するよりはよっぽど低負荷なのではなかろうか。
※負値はわかりにくいとの指摘があったのでそのうち調整します
~背景~
従来の種族値ベースの考え方に私は限界を感じている。
対戦中知りたいのは「あと何回の攻撃で相手は倒れるか」「次の攻撃で自分は倒れるか」ではなかろうか。
しかし、これを計算するためには「種族値」→「実値」→「ダメージ」→「割合」「回数」という順で計算しなくてはいけない。あっという間に60秒が過ぎる。
もっと別の指標で対戦時の優劣を表現できないものか。
次の攻撃で倒せるかどうか概算する方法がないか。
できるだけ簡単に。
~概要~
種族値などに代えて、それぞれのポケモン実値から画像の表のように評価値で表す。
(この表の求め方および数学的思考過程については次の記事で詳しく説明する)
例としてWCSルールシーズン3のポケモンTOP5は以下のようになる(0振り~252振り/性格補正なし)。
ウインディ
物理火力:☆-2.0~ ☆0.5
物理耐久:☆4.0~ ☆8.5
特殊火力:☆-2.5~ ☆0.0
特殊耐久:☆4.0~ ☆8.5
ガブリアス
物理火力:☆-0.5~ ☆1.5
物理耐久: ☆6.5~ ☆10.5
特殊火力:☆-4.5~ ☆-1.5
特殊耐久: ☆5.5~ ☆9.5
カプ・コケコ
物理火力:☆-1.5~ ☆1.0
物理耐久:☆3.0~ ☆8.0
特殊火力:☆-3.0~ ☆-0.5
特殊耐久:☆2.0~ ☆7.0
カプ・テテフ
物理火力:☆-4.0~ ☆-1.0
物理耐久:☆2.0~ ☆7.0
特殊火力:☆-0.5~ ☆1.5
特殊耐久:☆5.5~ ☆10.0
カミツルギ
物理火力:☆2.5~ ☆4.0
物理耐久:☆6.0~ ☆10.0
特殊火力:☆-7.0~ ☆-3.5
特殊耐久:☆-5.0~ ☆2.0
残念ながら、どのポケモンがどの程度の評価値なのかは種族値のように覚えなければならない。
この評価値で実際に計算してみる。計算は以下のルールで行う。
ルール①
相手の耐久評価値から、攻撃側の火力評価値を引く。
その時に0以下になれば倒せる事を意味する。
実例でやってみよう。
「カプ・コケコのかみなりで、ウインディを倒せるか」
カプ・コケコの極振りで☆-0.5、対してウインディの特殊耐久は無振りで4.0。
☆4.0から☆-0.5を引いて☆4.5、☆0より大きいので倒せない。
ちなみに割合を知りたい時は、計算結果によって大雑把に以下のようになる
☆0: HPの100%程度
☆1: HPの90%程度
☆2: HPの80%程度
☆3: HPの75%程度
☆4: HPの70%弱程度
☆5: HPの60%程度
また、確定数は引いた結果から以下のようになる。
~☆0 確1
~☆7 確2
~☆11 確3
~☆14 確4
今回は☆4.5なので相手HPを65%程度削って確2と言ったところか。
実際にダメ計すると
攻: カプ・コケコ Lv.50
防: ウインディ Lv.50
ダメージ: 93~109
割合: 56.3%~66%
回数: 確定2発
威力: 110
タイプ: でんき*/特殊
特攻: 147
特防: 100
最大HP: 165
で確かに最高乱数で66%になる。
ダメ―ジ乱数やその他もろもろの倍率は以下のように処理する。全部足し算引き算でできる。
ルール② 倍率計算時
2.0倍(弱点、2段階上昇等):☆7を足す
1.5倍(拘り、輝石、1段階上昇等):☆4を足す
1.3倍(珠等):☆3を足す
1.2倍(プレート等):☆2を足す
1.1倍(性格上昇補正等):☆1を足す
0.9倍(性格下降補正等):☆1を引く
2/3倍(威嚇、タイプ不一致、1段階下降等):☆4を引く
1/2倍(やけど、2段階下降等):☆7を引く
ルール③ 技の威力
120 攻撃側から☆1を足す
110 そのまま
100 攻撃側から☆1を引く
90 攻撃側から☆2を引く
80 攻撃側から☆3を引く
75 攻撃側から☆4を引く
ルール④ ダメージ乱数
低乱数(5%程度):そのまま
中乱数(30%程度):攻撃側から☆0.5を引く
中乱数(60%程度):攻撃側から☆1.0を引く
高乱数(90%程度):攻撃側から☆1.5を引く
実例でやってみよう。
「カプ・テテフがサイコフィールドを張っている。サイコキネシスでカミツルギを倒せるだろうか」
カプ・テテフの極振りで特殊火力は☆1.5、
サイキネは威力90なので☆2つ減らす→☆0.5
サイコフィールドの効果で1.5倍なので☆4つ増やす→☆4.5
半減なので☆7つ減らす→☆-3.5
高乱数で考えたいので☆1.5減らす→☆-5.0
カミツルギの特殊耐久は☆-5.0~☆2.0
カミツルギの特殊耐久が無振りであれば☆-5.0から☆-5.0を引いて☆0。
☆0はピッタリ確1くらいの打点ということ。
ダメ計すると
攻: カプ・テテフ Lv.50
防: カミツルギ Lv.50
ダメージ: 135~159
割合: 100.7%~118.6%
回数: 確定1発
技: サイコキネシス
威力: 135 [サイコ]
タイプ: エスパー*/特殊
特攻: 182
特防: 51
最大HP: 134
相性: ×0.5
丁度確1である。
恐らくこれまでとは全く異なる計算体系で慣れるまで抵抗もあるだろうし、
あくまで概算なのでギリギリの時には誤差を生じる恐れもある。
しかし、実戦では指折り数えることで計算できるので、
種族値ベースでダメ計するよりはよっぽど低負荷なのではなかろうか。
ベンチなし
2017年5月8日 ポケモンカードゲーム先日のジムバトルで、おぺらさんに見事ワンキルをくらい、その後も先行ファストレイドでワンキルされそうになった。
対戦相手の手腕が見事なのはモチロンのことだが、原因はこちらがベンチを出せなかったことにもある。
私のデッキには10枚のたねポケモンが入っているが、このデッキが最初の7枚でベンチにポケモンを置ける確率はいかほどなのか計算した。
まず、60枚の山札から7枚取り出すときの組み合わせ総数は combination(60, 7) で 386,206,920通りである。
デッキに10枚のたねポケモンをいれた時、個別にみてみると、組み合わせは以下の通り。
7枚中7枚がたねポケモン:120通り
7枚中6枚がたねポケモン:10,500通り
7枚中5枚がたねポケモン:308,700通り
7枚中4枚がたねポケモン:4,116,000通り
7枚中3枚がたねポケモン:27,636,000通り
7枚中2枚がたねポケモン:95,344,200通り
7枚中1枚がたねポケモン:158,907,000通り
7枚中0枚がたねポケモン:99,884,400通り
(合計386,206,920通り)
ポケモンカードゲームは、たねポケモンが手札にいない場合、もう一度引き直す(マリガン)。
マリガンは後の試行に影響を与えないため、「ゲームを開始できる時の手札」の組み合わせは単純に「7枚中0枚がたねポケモン」の組み合わせを除いた286,322,520通りである。
「ゲームを開始できる時の手札」のうち、ベンチにポケモンを出せないのは「7枚中1枚がたねポケモン」の時であるから、その確率は
158,907,000/286,322,520 = 0.55499302...
となり、およそ55.5%。
たねポケモンが10枚では、およそ2回に1回、ベンチにポケモンがいないことになる。
なお、たねポケモンがn枚の時、ベンチにポケモンがいない確率P(n)は以下のようになる。
P(n) = combination(60-n,6)*combination(n,1)/{combination(60,7)-combination(60-n,7)}
例えば、P(n) < 0.5にするためには12枚以上求められる。
対戦相手の手腕が見事なのはモチロンのことだが、原因はこちらがベンチを出せなかったことにもある。
私のデッキには10枚のたねポケモンが入っているが、このデッキが最初の7枚でベンチにポケモンを置ける確率はいかほどなのか計算した。
まず、60枚の山札から7枚取り出すときの組み合わせ総数は combination(60, 7) で 386,206,920通りである。
デッキに10枚のたねポケモンをいれた時、個別にみてみると、組み合わせは以下の通り。
7枚中7枚がたねポケモン:120通り
7枚中6枚がたねポケモン:10,500通り
7枚中5枚がたねポケモン:308,700通り
7枚中4枚がたねポケモン:4,116,000通り
7枚中3枚がたねポケモン:27,636,000通り
7枚中2枚がたねポケモン:95,344,200通り
7枚中1枚がたねポケモン:158,907,000通り
7枚中0枚がたねポケモン:99,884,400通り
(合計386,206,920通り)
ポケモンカードゲームは、たねポケモンが手札にいない場合、もう一度引き直す(マリガン)。
マリガンは後の試行に影響を与えないため、「ゲームを開始できる時の手札」の組み合わせは単純に「7枚中0枚がたねポケモン」の組み合わせを除いた286,322,520通りである。
「ゲームを開始できる時の手札」のうち、ベンチにポケモンを出せないのは「7枚中1枚がたねポケモン」の時であるから、その確率は
158,907,000/286,322,520 = 0.55499302...
となり、およそ55.5%。
たねポケモンが10枚では、およそ2回に1回、ベンチにポケモンがいないことになる。
なお、たねポケモンがn枚の時、ベンチにポケモンがいない確率P(n)は以下のようになる。
P(n) = combination(60-n,6)*combination(n,1)/{combination(60,7)-combination(60-n,7)}
例えば、P(n) < 0.5にするためには12枚以上求められる。
ラランテスGX+ゴルダックBreak
2017年5月6日 ポケモンカードゲームあんまりに訊かれる事が多いので、私のデッキについて少し書いておきます。
コンセプトはラランテスGXのワザ「フラワーサプライ」を使って場にエネルギーを溜め、ゴルダックBreakの特性「ハイパートランス」でエネルギーを管理するというもの。
そもそもはビビヨン(XY1)を使いたいというのが着想で、特に「カラフルウインド」は30+基本エネルギーの数x30ダメージと言う技で、最高打点300まで出ます。
ただ、多色が必須で管理が難しい。
ゴルダックBreakが色を問わないのが個性で、相手のHPに合わせてカラフルウインドの打点を調整できます。
相手の月輪の祭壇とかを逆利用できたりすると楽しいです。
コンセプトはラランテスGXのワザ「フラワーサプライ」を使って場にエネルギーを溜め、ゴルダックBreakの特性「ハイパートランス」でエネルギーを管理するというもの。
そもそもはビビヨン(XY1)を使いたいというのが着想で、特に「カラフルウインド」は30+基本エネルギーの数x30ダメージと言う技で、最高打点300まで出ます。
ただ、多色が必須で管理が難しい。
ゴルダックBreakが色を問わないのが個性で、相手のHPに合わせてカラフルウインドの打点を調整できます。
相手の月輪の祭壇とかを逆利用できたりすると楽しいです。
シャッフル
2017年5月2日 ポケモンカードゲーム
「N」や「サナ」を使うとシャッフルをしているにも関わらず手札がそのまま戻ってくることがある。
相手にもシャッフルをお願いしているが、それなのに戻ってくる。
対戦中の私のカードの混ぜ方はいわゆる「ヒンズーシャッフル」で、特に混ざらないシャッフルとして有名だが、
実際、戻した手札がどのようにして戻ってくるのか観察してみた。
ひたすらシャッフルして数えるという試行を繰り返し、結果以下の要領を得た。
【私のシャッフルの癖】
1. すべての手札を山札の一番上にまとめて戻す
2. 山札の中付近(上5~11枚から、下3~10枚の間)からまとめて引き抜き、上に持ってくる
3. 2.で上に持ってきた塊の上8~13枚を残し、下部を再び上に持ってくる
4. 3.で上に持ってきた塊の上7~11枚を残し、下部を再び上に持ってくる
以下繰り返し
ポイントは、2.以降は1.で引き抜いたカードをシャッフルしているだけで、
1.で引き抜かれなかったカード(およそ11~19枚)は全くシャッフルされていないということ。
最初に置いた手札もシャッフルされていないため、
この状態で相手に渡し、相手がカットした場合、運悪く山札の上に手札が戻って来うる。
相手が山札のどこを持ってカットするかが、二項分布に従うと仮定して、
1枚でも手札が戻って来る確率を計算してみた。
1点カットの場合0.67%、2点カットの場合48.58%となった。
そういえば妻と対戦している時、3回連続で手札が戻ってきたことがあったが、確かに妻はいつも3つに分けてカットする。
シャッフルの方法を変える必要がありそうだ。
相手にもシャッフルをお願いしているが、それなのに戻ってくる。
対戦中の私のカードの混ぜ方はいわゆる「ヒンズーシャッフル」で、特に混ざらないシャッフルとして有名だが、
実際、戻した手札がどのようにして戻ってくるのか観察してみた。
ひたすらシャッフルして数えるという試行を繰り返し、結果以下の要領を得た。
【私のシャッフルの癖】
1. すべての手札を山札の一番上にまとめて戻す
2. 山札の中付近(上5~11枚から、下3~10枚の間)からまとめて引き抜き、上に持ってくる
3. 2.で上に持ってきた塊の上8~13枚を残し、下部を再び上に持ってくる
4. 3.で上に持ってきた塊の上7~11枚を残し、下部を再び上に持ってくる
以下繰り返し
ポイントは、2.以降は1.で引き抜いたカードをシャッフルしているだけで、
1.で引き抜かれなかったカード(およそ11~19枚)は全くシャッフルされていないということ。
最初に置いた手札もシャッフルされていないため、
この状態で相手に渡し、相手がカットした場合、運悪く山札の上に手札が戻って来うる。
相手が山札のどこを持ってカットするかが、二項分布に従うと仮定して、
1枚でも手札が戻って来る確率を計算してみた。
1点カットの場合0.67%、2点カットの場合48.58%となった。
そういえば妻と対戦している時、3回連続で手札が戻ってきたことがあったが、確かに妻はいつも3つに分けてカットする。
シャッフルの方法を変える必要がありそうだ。
最初の7枚
2017年4月27日 ポケモンカードゲーム コメント (2)「n枚カードを入れた時、そのカードが最初の7枚の中に何枚あるか」、という期待値E(n)は
E(n) = Σ{i * combination(n, i) * combination(60-n, 7-i) / combination(60, 7)}
i = 0 → 7
であって、これを解くと
E(n) = 7n/60
が得られる。
一次関数E(n)について
E(n) >= 1 を満たすnは n >= 8.57...
E(n) >= 2 を満たすnは n >= 17.14...
となる。
最初の手札に1枚欲しければ9枚、2枚欲しければ18枚も入れねばならない。
E(n) = Σ{i * combination(n, i) * combination(60-n, 7-i) / combination(60, 7)}
i = 0 → 7
であって、これを解くと
E(n) = 7n/60
が得られる。
一次関数E(n)について
E(n) >= 1 を満たすnは n >= 8.57...
E(n) >= 2 を満たすnは n >= 17.14...
となる。
最初の手札に1枚欲しければ9枚、2枚欲しければ18枚も入れねばならない。
サイド落ち
2017年4月17日 ポケモンカードゲームm=(0,,,4)枚入れているカードが、山札にn枚残る(m-n枚がサイドに落ちる)確率p(m,n)は次の通り
p(m,n) = combination(60-m,6-m+n)*combination(m,m-n)/combination(60,6)
よって、m枚入れた時、デッキに残る期待値E(m)は
E(m) = Σ{n p(m,n)} n=0→4
となり、これを解くと以下の式が得られる。
E(m) = 0.9m
2枚以上入れれば、1枚以上デッキに残ることが期待できる。
p(m,n) = combination(60-m,6-m+n)*combination(m,m-n)/combination(60,6)
よって、m枚入れた時、デッキに残る期待値E(m)は
E(m) = Σ{n p(m,n)} n=0→4
となり、これを解くと以下の式が得られる。
E(m) = 0.9m
2枚以上入れれば、1枚以上デッキに残ることが期待できる。
戦略オートマトン
2017年4月5日6匹の中から先発に2匹、控えに2匹を選出する組み合わせ総数はcombin(6,2) * combin(4,2)で90通り。
相手も同様で、初期状態S0は90x90通り。
1ポケモンについて4通りのわざと2通りの交代、計6通りの戦略があり、2ポケモン分で6x6通り。
相手も同様で6^4通り。
樹形図のノードの最大数は、漸化式で表すと
S0 = 8100, Sn+1 = (6^4)*Sn
nターン後には
Sn = 25 * {4^(2 n - 1)} * 81^n
にまで膨れ上がる
相手も同様で、初期状態S0は90x90通り。
1ポケモンについて4通りのわざと2通りの交代、計6通りの戦略があり、2ポケモン分で6x6通り。
相手も同様で6^4通り。
樹形図のノードの最大数は、漸化式で表すと
S0 = 8100, Sn+1 = (6^4)*Sn
nターン後には
Sn = 25 * {4^(2 n - 1)} * 81^n
にまで膨れ上がる
ナマコブシ
2017年3月27日 ポケモンカードゲーム「れんぞくころがり」のような「裏が出るまでコイン試行を続けた時の表の期待値」という問題は高校数学で習う「無限等比級数の和」で求められる。
Sn = 0/2 + 1/2+2/4+3/8+・・・
0/2の項は0なので無視すれば、Snはa=1, r=1/2の無限等比級数であるから、その和は
Sn = 1/(1-(1/2)) = 2となり
表の期待値は2である。
水エネルギー1つで期待値60でるナマコブシの攻撃力は意外と侮れないのかもしれない。
Sn = 0/2 + 1/2+2/4+3/8+・・・
0/2の項は0なので無視すれば、Snはa=1, r=1/2の無限等比級数であるから、その和は
Sn = 1/(1-(1/2)) = 2となり
表の期待値は2である。
水エネルギー1つで期待値60でるナマコブシの攻撃力は意外と侮れないのかもしれない。
アローラの月光
2017年3月21日 ポケモンカードゲーム友人の購入分も合わせて42box1260pack中にカプ・テテフは41枚。
標本比率を41/1260 = 3.25%だとして、
183pack買えば"十中八九"テテフが4枚揃うことになる。
この標本から1packあたりのテテフのHit率も、
数学Bの「確率分布 」の知識で求められる。
ちなみに、"十中八九"で母比率を求めると、
1pack買ってテテフが当たる確率は2.53~3.97%といったところ。
標本比率を41/1260 = 3.25%だとして、
183pack買えば"十中八九"テテフが4枚揃うことになる。
この標本から1packあたりのテテフのHit率も、
数学Bの「確率分布 」の知識で求められる。
ちなみに、"十中八九"で母比率を求めると、
1pack買ってテテフが当たる確率は2.53~3.97%といったところ。
バトルコンプレッサーとピーピーマックス
2017年3月5日 ポケモンカードゲーム
山札から任意の3枚をトラッシュする「バトルコンプレッサー」。
山札から6枚引いて基本エネルギーがあればベンチにつけられる「ピーピーマックス」。
『圧縮すれば成功率が幾らなり上がるのは間違いないが、実際どれほど確率が上がるのか』
デッキの残り枚数をx、基本エネルギーの残り枚数がyとした時、ピーピーマックスの成功率p(x,y)は
p(x,y) = 1-combin(x-y,6) / combin(x, 6)
=1-(x-y)(x-y-1)(x-y-2)(x-y-3)(x-y-4)(x-y-5)/x(x-1)(x-2)(x-3)(x-4)(x-5)
同様にバトルコンプレッサー後の成功率p(x-3,y)は
p(x-3,y) = 1-combin(x-y-3,6) / combin(x-3, 6)
=1-(x-y-3)(x-y-4)(x-y-5)(x-y-6)(x-y-7)(x-y-8)/(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)
今回は差で評価する。成功率の増差はp(x,y)-p(x-3,y)。
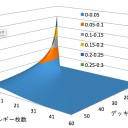
これは二変数の関数で、等高線グラフで表すと画像の通り。
グラフの大多数を占める青い領域は上昇率が5%以下のところ。
山札が多い時は全て青く、例えば山札が45枚でエネ7枚の場合、
ピーピーマックスを単発で使うと成功率は66.1%
3枚圧縮して69.1%で3%しか上がらない。
もし山札17枚、エネ2枚だとすると単発の成功率は59.6%、
圧縮すると69.2%で約10%upする。
ただし、山札が減っていれば良いというわけではなく、
もし17枚中、エネが7枚残っていると、単発で98.3%。
圧縮して99.7%で、効果は1%以下。
圧縮してもしなくても変わらない。
『山札が減ってきていて、更に残りのエネも減ってきている時が望ましく、その時1割程度成功率が上がる』
山札からトラッシュに移動する効果は良いが、圧縮という点では効果は限定的なのかもしれない。
山札から6枚引いて基本エネルギーがあればベンチにつけられる「ピーピーマックス」。
『圧縮すれば成功率が幾らなり上がるのは間違いないが、実際どれほど確率が上がるのか』
デッキの残り枚数をx、基本エネルギーの残り枚数がyとした時、ピーピーマックスの成功率p(x,y)は
p(x,y) = 1-combin(x-y,6) / combin(x, 6)
=1-(x-y)(x-y-1)(x-y-2)(x-y-3)(x-y-4)(x-y-5)/x(x-1)(x-2)(x-3)(x-4)(x-5)
同様にバトルコンプレッサー後の成功率p(x-3,y)は
p(x-3,y) = 1-combin(x-y-3,6) / combin(x-3, 6)
=1-(x-y-3)(x-y-4)(x-y-5)(x-y-6)(x-y-7)(x-y-8)/(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)
今回は差で評価する。成功率の増差はp(x,y)-p(x-3,y)。
これは二変数の関数で、等高線グラフで表すと画像の通り。
グラフの大多数を占める青い領域は上昇率が5%以下のところ。
山札が多い時は全て青く、例えば山札が45枚でエネ7枚の場合、
ピーピーマックスを単発で使うと成功率は66.1%
3枚圧縮して69.1%で3%しか上がらない。
もし山札17枚、エネ2枚だとすると単発の成功率は59.6%、
圧縮すると69.2%で約10%upする。
ただし、山札が減っていれば良いというわけではなく、
もし17枚中、エネが7枚残っていると、単発で98.3%。
圧縮して99.7%で、効果は1%以下。
圧縮してもしなくても変わらない。
『山札が減ってきていて、更に残りのエネも減ってきている時が望ましく、その時1割程度成功率が上がる』
山札からトラッシュに移動する効果は良いが、圧縮という点では効果は限定的なのかもしれない。