マッドマウンテンとしょうりのほし

コインを2枚投げてその両方がオモテになる確率は

1/2 x 1/2 = 1/4

で25%である。

もし、この時、ウラが出た時に一度だけコインを投げなおして良いとなった場合の確率は幾らだろうか。

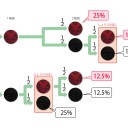
今回は試行回数が少ないので樹形図で見てみる。

1度の降り直しが可能な状態で、2度のコイントスの結果は図の通り6パターンになる。

A. 1枚目が表、2枚目も表
B. 1枚目が表、2枚目が裏で、振りなおして表
C. 1枚目が表、2枚目が裏で、振りなおして裏
D. 1枚目が裏で、振りなおして表、2枚目が表
E. 1枚目が裏で、振りなおして表、2枚目が裏
F. 1枚目が裏で、振りなおしても裏


このうち、2回とも表になるパターンは以下の3つ

A. 1枚目が表、2枚目も表
B. 1枚目が表、2枚目が裏で、振りなおして表
D. 1枚目が裏で、振りなおして表、2枚目が表

判定はコイントスのみで、その確率は他に影響されず、常に1/2であるから、
投げたコインの回数nとして、それぞれの状態になる確率は「1/2のn乗」である。

すなわち、それぞれ

A. (1/2)^2 = 1/4 = 25%
B. (1/2)^3 = 1/8 = 12.5%
D. (1/2)^3 = 1/8 = 12.5%

よって、表題の成功率は、25%+12.5%+12.5%=50%

ビクティニがいれば、サイドンのマッドマウンテンを、コイントス1回分で成功させられるわけだ。